ASSESSING OBSERVER AGREEMENT WHEN DESCRIBING AND CLASSIFYING FUNCTIONING WITH THE INTERNATIONAL CLASSIFICATION OF FUNCTIONING, DISABILITY AND HEALTH
Eva Grill, DrPH, MPH1, Ulrich Mansmann, PhD2, Alarcos Cieza, MPH1 and Gerold Stucki, MD, MS1,3
From the 1ICF Research Branch, WHO FIC Collaborating Center (DIMDI), Institute for Health and Rehabilitation Sciences, 2Department of Medical Informatics, iometry and Epidemiology and 3Department of Physical Medicine and Rehabilitation, University of Munich, Munich, Germany
OBJECTIVE: The International Classification of Functioning, Disability and Health (ICF) is used increasingly to describe and classify functioning in medicine without being a psychometrically sound measure. All categories of the ICF are quantified using the same generic 0–4 scale. The objective of this study was to assess observer agreement when describing and classifying functioning with the ICF.
DESIGN: A second-level category of the ICF, d430 lifting and carrying objects, was used as an example. To the qualifiers of this category, clinically meaningful definitions were assigned. Data were collected in a cross-sectional survey with repeated measurement. We report raw, specific and chance-corrected measures or agreement, a graphical method and the results of log-linear models for ordinal agreement.
SUBJECTS/PATIENTS: A convenience sample of patients requiring physical therapy in an acute hospital.
RESULTS: Twenty-five patients were assessed twice by 2 observers. Raw agreement was 0.52. Kappa was 0.36, indicating fair agreement. Different hierarchical log-linear models indicated that the strength of agreement was not homogeneous over all categories.
CONCLUSION: Observer agreement has to be evaluated when describing and classifying functioning using the ICF Qualifiers’ scale. When assessing inter-observer reliability, the first step is to calculate a summary statistic. Modelling agreement yields valuable insight into the structure of a contingency table, which can lead to further improvement of the scale.
Key words: reproducibility of results, rehabilitation, rater agreement, ICF, log linear models.
J Rehabil Med 2007; 39: 71–76
Correspondence address: Gerold Stucki, Department of Physical Medicine and Rehabilitation, University of Munich, Marchioninistr. 15, DE-81377 Munich, Germany. E-mail: gerold.stucki@med.uni-muenchen.de
Submitted February 6, 2006; accepted August 18, 2006.
Introduction
The International Classification of Functioning, Disability and Health (ICF) is used increasingly to universally describe and classify functioning in medicine (1, 2). The basis for the application of the ICF, both in clinical practice and research, are practical tools, such as the ICF Core Sets (3–6). The ICF is not a psychometric measure with established objectivity, reliability, validity and sensitivity. Nevertheless, the extent of the patients’ impairments in body functions, limitations in activities, and restrictions in participation, as well as the extent to which environmental factors represent barriers or facilitators for the patients’ functioning, are classified with the ICF Qualifier on an ordinal scale.
All categories of the ICF are quantified using the same generic 0–4 scale with qualifier 0 representing no problem and qualifier 4 representing that the problem is complete (7). A moderate problem (qualifier 2) is defined as up to half of the time or half the scale of total difficulty. Accordingly, qualifier 1 represents 5–24% of total difficulty and qualifier 3, 50–95% of total difficulty. The World Health Organization (WHO) encourages calibrating those qualifiers against already existing measures. Equally, the WHO encourages the development of clinical standards and the assignment of clinically meaningful and appropriate wording to the existing qualifier frame.
Any prospective user is faced with the question of reliability when using the ICF qualifiers in research, clinical practice and quality management. Sufficient reliability means that 2 observers will effectively come to the same result when observing the same attribute by the same scale. One of the reasons to assess agreement is that it enables us to draw inferences about the quality of the scale and the accuracy of diagnosis. Errors in measurement or misclassification may result in substantial bias in estimated effects, impaired precision, and in distortion of the p-values of the corresponding significance tests (8, 9).
There are a number of methods to assess the agreement of ordinal data. They include single indices of agreement, such as adapted correlation coefficients and the kappa coefficient (10), which is a commonly-used measure in biomedical research. Be aware that common correlation coefficients are not suitable to measure agreement because correlation may be unaffected by a systematic disagreement (11). Measures of concordance and discordance (12, 13) make use of the specific properties of ordinal data and are equally useful for low or zero cell frequencies and small data sets. Single indices of agreement do, however, have limitations. Indices of agreement are artificially lower in populations with a restricted spectrum of the measured characteristic (14, 15). There are methods to examine observer agreement graphically (11, 16) in a more explorative way, e.g. by drawing receiver operating characteristic (ROC) curves (17). Modelling the structure of agreement – using, for example, log-linear models – may be an elegant, but not obvious, solution permitting for a multitude of simple or complex situations that may appear in the cross-classified observer ratings (18, 19). Finally, latent class analysis is a most promising tool for the interpretation of diagnostic accuracy on a dichotomous or an ordinal scale (20, 21) and for estimation of the true prevalence of impairment from a pair of imperfect ratings. These approaches are not new and all of them have been reported in the statistical literature in one form or the other.
There are a number of possible reasons for low observer agreement or low agreement in repeated ratings by a single observer. Low agreement can be due to flawed operationalization of the concepts to be measured, to a change in the tested patient, or to the differing evaluation capacity of the 2 observers or of the same observer at 2 different points in time. These reasons, which are especially important to study in a new scale, can be explored by examining cross-tabulations and plots and by modelling.
The objective of this study was to assess the observer agreement when describing and classifying functioning with the ICF.
Methods
Study design and data collection procedures
The study design was a cross-sectional survey with repeated measurement in a convenience sample of patients with neurological, musculoskeletal and cardiopulmonary conditions requiring physical therapy in an acute hospital. Patients were recruited consecutively in the University Hospital Zurich between June and October 2004.
Patients were recruited and assessed by physical therapists trained in the application and principles of the ICF. Assessment was to be repeated by a second physical therapist after a minimum of 24 hours and a maximum of 36 hours. This was to ensure that the patients’ condition did not change substantially between first and second assessment.
Measures
The ICF has 2 parts, each containing 2 separate components. Part 1 covers functioning and disability and includes the components Body Functions (b), Body Structures (s), and Activities and Participation (d). Part 2 covers contextual factors and includes the components Environmental Factors (e) and Personal Factors. In the ICF classification, the letters b, s, d, and e, which refer to the components of the classification, are followed by a numeric code starting with the chapter number (1 digit) followed by the second level (2 digits), and the third and fourth levels (1 digit each). For this study, a second-level category of the ICF, the ICF category d430 lifting and carrying objects was used.
To the qualifiers of this category clinically meaningful definitions were assigned by a group of physical therapists who were experienced in assessment and experts in the evaluation of rating scales. The ICF qualifiers’ scale for the ICF category d430 lifting and carrying objects, which will be used as an example throughout, was defined as follows: 0=patient is able to lift and carry heavy objects, 1=patient is able to lift a heavy object, 2=patient is able to lift and carry a light object (e.g. a bottle), 3=patient is able to lift a light object, 4=patient is not able to lift or to carry.
Statistical analyses
Raw, specific and chance-corrected measures or agreement. Overall raw agreement can be calculated by dividing the sum of the frequencies of the main diagonal of a contingency table by the sample size. The proportion of agreement specific to one response category is calculated by dividing twice the frequency of agreement about this response category by the sum of row and column totals for this response category (22). The proportion of agreement specific to one response category gives information on which response categories are easily agreed and which are not. Both raw and specific measures, however, do not take agreement by chance into consideration.
The kappa coefficient (10) expresses agreement as the observed proportion of agreement corrected for chance. As with other measures of agreement kappa ranges between –1 and 1. For ratings on an ordinal scale, weighted kappa respects the ordering of the categories. Disagreement between 2 adjacent categories contributes less to the weighted kappa coefficient as disagreement defined by a rating based on the lower and upper extreme category. Thus, cell frequencies are considered in terms of their distance to the main diagonal. The weighted kappa coefficient varies depending on the weight type. The Cicchetti & Allison weight uses the distance to the main diagonal (23); the Fleiss & Cohen weight uses the squared distance (24). A kappa value of 0.81–1.00 is defined as almost perfect agreement, 0.61–0.80 as substantial, 0.41–0.60 as moderate, 0.21–0.40 as fair, 0.00–0.20 as slight and values below 0.00 as poor agreement (25). Confidence intervals can be calculated based on the estimates of the asymptotic standard error for large samples for both kappa and weighted kappa. Kappa provides a good over-all estimate of the chance-corrected agreement. Kappa, however, reduces the data to a single number which can be interpreted only if the underlying contingency table is also examined and the clinical context considered.
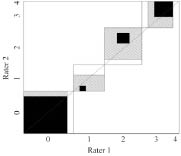
Graphical methods. The Bangdiwala observer agreement chart (16, 26) is a way to represent the strength of agreement in a contingency table. The Bangdiwala chart gives a square whose edges represent sample size. Within a large square (total sample) there are as many small rectangles as there are categories. Those small rectangles are aligned along the main diagonal. Within the small rectangles there are black squares that show observed agreement. The edges of those black squares are determined by the number of equal ratings for a specific category. Partial agreement can be shown by showing agreement in off-diagonal cells, yielding hatched areas. To give an example (see Fig. 2), both observer 1 and observer 2 rated 8 patients as able to lift and carry heavy objects (category 0), but they agreed only about 7 patients. Thus the small rectangle is of size 8×8, whereas the black square within is of size 7×7. Observer 1 rated one patient into category 1 who was rated into category 0 by observer 2. Category 1 is still close to category 0 so there is a hatched rectangle of size 8×7 within the small rectangle. Evaluating the position of the squares can easily discover any imbalance between observers or between response categories. For example, the departure of the black square from the main diagonal in category 1 indicates that, in this category, observer 1 tends to rate patients as more severely impaired than observer 2 (4 of 5 have category 2 or worse for observer 1 vs 3 of 5 for observer 2).
Models for ordinal agreement data. Log-linear models give information on how the expected cell count in contingency tables depends on levels of the categorical variables for that cell, as well as on associations and interactions among those variables. When modelling contingency tables, log-linear models deal with aggregated data. Log-linear models for ordinal agreement data try to decompose the different aspects of agreement into distinct components (27, 28). Several separate models are fit to the data. They allow to pose specific question (Is disagreement symmetric to the main diagonal? Is disagreement more distinct for higher categories?) to the data and to test specific hypotheses.
First, there is the overall agreement. Any analysis of contingency tables starts with the hypothesis that there is no association between the 2 variables representing observer ratings. This can be expressed by a log-linear model that formalizes the independence of the 2 observers’ ratings by 2 main effects only (M0: f~obs.1+obs.2, meaning that the row variable obs.1 is independent of column variable obs.2). This independence model takes into account random agreement between 2 observers but it is not suited to formalize possible forms of agreement or disagreement. An interaction term of varying complexity can be used to address this issue (M1: f~obs.1+obs.2+Ind). This includes a component representing chance (obs.1 + obs.2) and another component representing agreement (Ind). It takes into consideration that the 2 observers assessed the same patients and that there is a tendency for both observers to give a rating of high impairment if the patient is highly impaired.
A model including a special form of the interaction term, the agreement model, consists in adding one more parameter to the independence model counting the surplus of observations given on the main diagonal (M1: f~obs.1+obs.2+Indi = j). This model assumes that the strength of association is constant throughout the categories. Agreement is as good about low response categories as about high response categories.
The obvious extension, called the uniform association model uses an individual parameter for each cell on the main diagonal: for example if observers agree about low response categories, but not about high response categories (M2: f~obs.1+obs.2+Indi = j = 0+…+ Indi = j = 4). Schuster & von Eye (19) presented a model which adds parameters for the varying effects of the different response categories to the parameters of the uniform association model and the agreement model.
Additionally, other parameters can be added to allow for varying degrees of local association and forms of disagreement: symmetric disagreement around the main diagonal (M3: f~obs.1+obs.2+ Ind |i-j| = 0 +…+ Ind |i-j| = 4), or non-symmetric disagreement (M4: f~obs.1+obs.2+ Indi-j = -4 +…+ Ind i-j = 4). Model selection procedures can be used to search for the most appropriate model description of the data and to clarify agreement structure.
For each aspect of agreement a separate model can be fitted. As the models are built to be hierarchical, they can be compared with each other by the goodness-of-fit statistics or likelihood ratio tests. Non-hierarchical models can equally be compared by using the Akaike Information Criterion (AIC, AIC= –2logLikelihood + 2(n–df)). The lower the AIC, the better the fit. To examine the agreement structure of the ICF category lifting and carrying objects SAS Proc genmod with the log link function assuming Poisson distribution was used. We modelled the contingency table presented in Fig. 1.
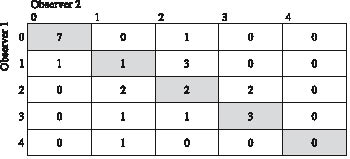
Fig. 1. Contingency table of the observer agreement for ICF category d430 (to lift and carry objects). 0=patient is able to lift and carry heavy objects, 1=patient is able to lift a heavy object, 2=patient is able to lift and carry a light object (e.g. a bottle), 3=patient is able to lift a light object, 4=patient is not able to lift or to carry. Cells on the main diagonal are shaded grey, representing the patients about whom the observers agreed.
Results
In total, 25 patients were assessed twice by 2 observers.
Raw agreement was 0.52 (13/52), indices for specific agreement were 0.88 (response category 0: 14/18), 0.20 (response category 1: 2/10), 0.31 (response category 2: 4/13), 0.60 (response category 3: 6/10) and 0 (response category 4: 0/1). Kappa was 0.36, indicating fair agreement (95% confidence interval [0.11–0.61]), weighted kappa was 0.51 (95% confidence interval [0.27–0.76]) when the Cicchetti & Allison weight (23) was applied, and 0.63 (95% confidence interval [0.37–0.89]) when the Fleiss & Cohen weight (24) was applied, indicating moderate agreement.
Fig. 1 shows the contingency table along with the specific operationalization of the ICF qualifiers‘ scale. Cells on the main diagonal are shaded grey. They represent the patients about whom the observers agreed.
Fig. 2 shows the Bangdiwala agreement chart. This indicates that there was no systematic deviation from the main diagonal, i.e. no systematic difference in observers‘ rating. Agreement seemed to be best for categories 0, 1 and 4, whereas observers had difficulties to differentiate between 2 and 3.
Fig. 2. Bangdiwala observer agreement chart for ICF-category d430. The chart is a square whose edges are determined by sample size. The edges of the black squares show the number of patients who got identical ratings from both observers. The large bright rectangle shows the maximum possible agreement, given the marginal totals. Partial agreement is showed by including a weighted contribution from off-diagonal cells, here represented by hatching. One observer’s ratings would differ systematically from the other observer’s ratings if all black squares were above or below the diagonal.
Observer 2
0 1 2 3 4
0 1 2 3 4
Observer 1
Different hierarchical log-linear models were evaluated. We assessed the independence model (M0: f~obs.1+obs.2), the agreement model (M1: f~obs.1+obs.2+Indi = j) and the model as proposed by Schuster & von Eye (19) to evaluate the specific structure of the contingency table (M2: f~obs.1+obs.2+Indi = j = 0+…+ Indi = j = 4). The best fit is given by model M2 assuming varying agreement over the main diagonal (AICM2=36.06, AICM1=41.26, AICM0=46.02). The likelihood ratio test shows a clear superiority of Model M1 over Model M0 (χ2 = 8.7605, DF=1, p=0.0031). Also, the likelihood ratio test shows a clear superiority of Model M2 over Model M1 (χ2=13.2013, DF=4, p=0.0103). Therefore, the strength of agreement seems not to be homogeneous over all categories. Looking at the data it seems to be interesting to suppose differences in agreement between category 0 and the rest. The model M1* is formalizing this idea (M1*: f~obs.1+obs.2+Indi = j = 0+ Indi = j; i = 1,…, 4). The AICM1* is 34.07, the smallest under the models studied so far. Comparing the hierarchical models M1, M1*, and M2 by likelihood ratio test shows a significant gain of model fit between M1 and M1* (χ2=9.1894, DF = 1, p=0. 0.0024), but not between M1* and M2 (χ2=4.0119, DF=3, p=0.2602). This indicates different concepts when assessing category 0 compared with the assessment of the other categories by the observers under study.
Additionally, models were fitted assuming symmetric disagreement (M3: f~ Ind |i-j| = 0 +…+ Ind |i-j| = 4). and non-symmetric disagreement (M4: f~ Indi-j = -4 +…+ Ind i-j = 4) around the main diagonal. The model with symmetric disagreement has a lower AIC than the model assuming non-symmetric disagreement (AICM3=42.19, AICM4=46.75). There was no evidence that disagreement is systematically different between both observers resulting in systematically higher or lower ratings by one of the observers.
A summary of the results, along with their interpretation, is given in Table I.
| Table I. Examples of methods and results to assess agreement on an ordinal scale along with their interpretation | ||
| Method | Result | Interpretation |
| Raw agreement | p=0.52 | Observers assigned to 52% of the patients the same rating |
| Chance-corrected agreement | kappa=0.36 | There was more agreement between the 2 observers than would be expected by chance alone. Agreement was fair. |
| Graphical methods | See Fig. 1 | There was no systematic difference in observers’ rating. Agreement seemed to be best for categories 1 and 4, whereas observers had difficulty differentiating between categories 2 and 3. |
| Log-linear modelling | Akaike Information Criterion (AIC) indicates model fit. The lower AIC in comparison with the degrees of freedom used by the model the better the model fit. | |
| Fit of the independence model AIC=46.02 | There was a statistically significant association between the 2 observers’ ratings. | |
| Fit of the agreement model AIC=41.26 | There is agreement, but strength of agreement seems not to be homogenous across categories. A substantial proportion of ratings is contained in the main diagonal. | |
| Specific structure of the contingency table AIC=36.06 | Agreement varied with different response categories. | |
| Difference in agreement between category 0 and the rest AIC=34.07 | Agreement varied with different response categories. There are different concepts when assessing category 0 compared with the assessment of the other categories. | |
| Symmetric disagreement AIC=42.19 Asymmetric disagreement AIC=46.75 | There is no evidence that disagreement is systematically different between both observers resulting in systematically higher or lower ratings by one of the observers | |
Discussion
The example presented in this paper clearly demonstrates the need to assess the observer agreement when describing and classifying functioning using the ICF Qualifiers’ scale. It has been popular to measure agreement on a nominal scale using kappa and on an ordinal scale using weighted kappa. When interpreting the results of the kappa statistic, a high kappa seems to be proof of a sound process. There is, however, a multitude of reasons why kappa may not be a reliable summary measure (14, 18, 29). Still, a low kappa requires attention regarding possible reasons. Our example showed only moderate agreement between observers when looking at the kappa statistic. Apart from the obvious, i.e. flawed operationalization of measured concepts, possible reasons include very high or very low prevalence of the measured characteristic, a change in the tested individual or systematic differences in observers’ evaluation capacity. Reasons for inconsistency in observers’ ratings can be discovered by only methods yielding more differentiated results (29). By examining plots such as the Bangdiwala agreement chart, we could show that there was no systematic difference between observers, indicating that the lack of agreement (as indicated by the kappa statistic) was most probably due to the operationalization of the rating scale studied.
Agreement models showed that strength of agreement seemed not to be homogeneous over all categories. In general, the data gave the impression that the observers were able to differentiate between a patient who was not impaired in lifting and carrying (qualifier 0) and a patient who was impaired in this respect. Within the group of impaired patients they were not able to easily distinguish between patients being able to lift heavy objects (qualifier 2) and patients being able to lift and carry light objects (qualifier 3). It could be argued that these 2 response categories, indeed, blend 2 different concepts. This example indicates that modelling agreement yields valuable insight into the structure of a contingency table which can lead to further improvement of the scale (27).
The value of the different approaches presented here also consists of its applicability to any ICF category and to any operationalization of the ICF Qualifiers’ scale. The WHO does not provide any specific definition for each of the response categories of the qualifiers’ scale. It exclusively provides broad ranges of percentages in a scale of total difficulty, total problem, or total impairment for each of the ICF categories. The ICF Checklist, to give an example, provides a selection of ICF categories to elicit and record information on the functioning and disability of an individual. Its proposed qualifiers might be difficult to record and to interpret, such as “1 = Mild impairment means a problem that is present less than 25% of the time, with an intensity a person can tolerate and which happens rarely over the last 30 days” (30). It would also be worthwhile to perform the analyses presented in this paper when those broad ranges of percentages or definitions given by the ICF Checklist are the only operationalization of the qualifiers’ scale provided to the users of the ICF.
A limitation of our study is the very small sample size. This results in very large interval estimates of the kappa statistics, as well as in decreased precision for modelling and probabilistic interval estimation. This example, however, also shows that more sophisticated methods for the analysis of agreement can also be applied on sparse data, as long as the limitations of the results are made clear.
Another limitation is the involvement of only 2 observers. Indeed, the kappa statistic could also be used with more than 2 observers. Equally, all other methods can easily be extended for ratings of more than 2 observers (31). There is a whole group of latent class analysis which require data from at least 3 observers (21) or from multiple populations with varying prevalences (32).
In our study, agreement between the 2 observers was only moderate. This was due to the imperfect operationalization of 2 of the qualifiers. As a consequence, for this ICF category several options are possible: first, collapsing the existing operationalization for it to result into a scale with 3 qualifiers; secondly, discarding the operationalization and restart with a dichotomized item which gives information only on presence or absence of impairment; thirdly, redoing the operationalization of the doubtful qualifiers. The option to be preferred will depend on the specific aims of any study or clinical assessment. Accordingly, it depends on the purpose of the assessment if moderate agreement about a characteristic is acceptable as it is.
In conclusion, the potential user of the qualifier structure of the ICF has to be aware of the potential drawbacks of any operationalization. When assessing inter-observer reliability the first step is to calculate a summary statistic. These coefficients and their interpretation are well known. It may be useful, however, to use more refined methods than the kappa statistic to assess reliability between 2 or more observers.
Low agreement will stimulate researches to explore possible reasons. Cross-tabulations, appropriately applied and interpreted plots, and modelling may provide valuable insights and help to improve the scale under examination.
AcknowledgEment
This analysis makes use of data from the t-pathways project undertaken by the Department of Rheumatology and Institute of Physical Medicine, University Hospital Zurich, Switzerland. Our cordial thanks go to the project leader, Erika Omega Huber.
References
1. Stucki G, Cieza A, Ewert T, Kostanjsek N, Chatterji S, Üstün TB. Application of the International Classification of Functioning, Disability and Health (ICF) in clinical practice. Disabil Rehabil 2002; 24: 281–282.
2. Stucki G, Ewert T, Cieza A. Value and application of the ICF in rehabilitation medicine. Disabil Rehabil 2002; 24: 932–938.
3. Cieza A, Ewert T, Üstün TB, Chatterji S, Kostanjsek N, Stucki G. Development of ICF Core Sets for patients with chronic conditions. J Rehabil Med 2004; 36: 9–11.
4. Grill E, Ewert T, Chatterji S, Kostanjsek N, Stucki G. ICF Core Set development for the acute hospital and early post-acute rehabilitation facilities. Disabil Rehabil 2005; 27: 361–366.
5. Stucki G, Grimby G. Applying the ICF in medicine. J Rehabil Med 2004; 36: 5–6.
6. Üstün B, Chatterjii S, Kostanjsek N. Comments from WHO for the Journal of Rehabilitation Medicine special supplement on ICF Core Sets. J Rehabil Med 2004; 36: 7–8.
7. World Health Organisation. International Classification of Functioning, Disability and Health: ICF. Geneva: WHO; 2001.
8. Kupper LL. Effects of the use of unreliable surrogate variables on the validity of epidemiologic research studies. Am J Epidemiol 1984; 120: 643–648.
9. Quade D, Lachenbruch PA, Whaley FS, McClish DK, Haley RW. Effects of misclassifications on statistical inferences in epidemiology. Am J Epidemiol 1980; 111: 503–515.
10. Cohen J. A coefficient of agreement for nominal scales. Educ Psychol Meas 1960; 20: 37–46.
11. Bland J, Altman D. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1986; 1: 307–310.
12. Svensson E. Ordinal invariant measures for individual and group changes in ordered categorical data. Stat Med 1998; 17: 2923–2936.
13. Svensson E. Concordance between ratings using different scales for the same variable. Stat Med 2000; 19: 3483–3496.
14. Feinstein AR, Ciccetti DV. High agreement but low kappa: I. The problems of two paradoxes. J Clin Epidemiol 1990; 43: 543–549.
15. Guggenmoos-Holzmann I. The meaning of kappa: probabilistic concepts of reliability and validity revisited. J Clin Epidemiol 1996; 49: 775–782.
16. Bangdiwala K. Using SAS software graphical procedures for the observer agreement chart. Proceedings of the SAS User’s Group International Conference, 1987: 1083–1088.
17. Svensson E, Holm S. Separation of systematic and random differences in ordinal rating scales. Stat Med 1994; 13: 2437–2453.
18. Guggenmoos-Holzmann I, Vonk R. Kappa-like indices of observer agreement viewed from a latent class perspective. Stat Med 1998; 17: 797–812.
19. Schuster C, von Eye A. Models for ordinal agreement data. Biom J 2001; 43: 795–808.
20. Joseph L, Gyorkos TW, Coupal L. Bayesian estimation of disease prevalence and the parameters of diagnostic tests in the absence of a gold standard. Am J Epidemiol 1995; 141: 263–272.
21. Uebersax JS, Grove WM. Latent class analysis of diagnostic agreement. Stat Med 1990; 9: 559–572.
22. Spitzer RL, Fleiss JL. A re-analysis of the reliability of psychiatric diagnosis. Br J Psychiatry 1974; 125: 341–347.
23. Cicchetti D, Allison T. A new procedure for assessing reliability of scoring EEG sleep recordings. Am J EEG Technol 1971; 11: 101–109.
24. Fleiss J, Cohen J. The equivalence of weighted kappa and the intraclass correlation coefficient as measures of reliability. Educ Psychol Meas 1973; 33: 613–619.
25. Landis J, Koch G. The measurement of observer agreement for categorical data. Biometrics 1977; 33: 159–174.
26. Friendly M. Visualising categorical data. Cary, NC: SAS Institute; 2000.
27. Agresti A. A model for agreement between ratings on an ordinal scale. Biometrics 1988; 44: 539–548.
28. Tanner MA, Young MA. Modeling ordinal scale disagreement. Psychol Bull 1985; 98: 408–415.
29. Guggenmoos-Holzmann I. How reliable are chance-corrected measures of agreement? Stat Med 1993; 12: 2191–2205.
30. World Health Organization. ICF Checklist Version 2.1a, Clinical Form for International Classification of Functioning, Disability and Health: ICF. Geneva: WHO; 2001.
31. Walter SD, Irwig LM. Estimation of test error rates, disease prevalence and relative risk from misclassified data: a review. J Clin Epidemiol 1988; 41: 923–937.
32. Hui SL, Walter SD. Estimating the error rates of diagnostic tests. Biometrics 1980; 36: 167–171.
