Asaduzzaman Khan, PhD1, Chi-Wen Chien, PhD2 and Karl S. Bagraith, BoccThy(Hons)1,3

From the 1School of Health and Rehabilitation Sciences, The University of Queensland, Brisbane, Australia, 2Department of Rehabilitation Sciences, The Hong Kong Polytechnic University, Hung Hom, Kowloon, Hong Kong (SAR), China and 3Interdisciplinary Persistent Pain Centre, Gold Coast Hospital and Health Service, Gold Coast, Australia

OBJECTIVE: To investigate whether using a parametric statistic in comparing groups leads to different conclusions when using summative scores from rating scales compared with using their corresponding Rasch-based measures.

METHODS: A Monte Carlo simulation study was designed to examine between-group differences in the change scores derived from summative scores from rating scales, and those derived from their corresponding Rasch-based measures, using 1-way analysis of variance. The degree of inconsistency between the 2 scoring approaches (i.e. summative and Rasch-based) was examined, using varying sample sizes, scale difficulties and person ability conditions.

RESULTS: This simulation study revealed scaling artefacts that could arise from using summative scores rather than Rasch-based measures for determining the changes between groups. The group differences in the change scores were statistically significant for summative scores under all test conditions and sample size scenarios. However, none of the group differences in the change scores were significant when using the corresponding Rasch-based measures.

CONCLUSION: This study raises questions about the validity of the inference on group differences of summative score changes in parametric analyses. Moreover, it provides a rationale for the use of Rasch-based measures, which can allow valid parametric analyses of rating scale data.

Key words: rating scales; parametric statistics; Rasch analysis; simulation; summative scores; Rasch-based measures.

J Rehabil Med 2015; 47: 00–00

Correspondence address: Asad Khan, School of Health and Rehabilitation Sciences, The University of Queensland, Brisbane QLD 4072, Australia. E-mail: a.khan2@uq.edu.au

Accepted Nov 5, 2014; Epub ahead of print Feb 13, 2015

Introduction

Clinicians and researchers in health and rehabilitation sciences often need to assess patient-reported outcomes that may not be directly measurable; for example, disability, cognitive function, quality of life, satisfaction, or pain intensity. Such patient-reported outcomes are often measured indirectly via their manifestations, and are referred to as “latent variables”, “latent traits” or “constructs” (1, 2). Ordinal rating scales are commonly employed to quantify latent traits or constructs. In ordinal rating scales, respondents choose from a series of ordered response options, which generally denote “less” or “more” of a construct (e.g. in measuring pain, none = 0, mild = 1, moderate = 2 and severe = 3). However, responses on such scales simply represent an ordinal graduation, rather than a “real number” or “physical magnitude” with inherent meaning (measurement scales are described in (3)). In addition, a change or difference of 1 point on ordinal scales can vary in meaning across the scale’s continuum (4). Thus, ordinal rating scales do not typically produce interval-level data, and the mathematical manipulations (e.g. addition, substraction, or mean) that are routinely applied to ordinal scores in order to assess patient outcomes may not have readily interpretably meaning within or between patients (5, 6).

Rating scales are widely used to assess patient-reported outcomes that are complex in nature. These items can be pooled to generate a single summary score, which is meant to measure the phenomenon quantified by the set of items. Sometimes the items are weighted or standardized before pooling; however, the most common strategy to generate summary scores is via direct summation of the relevant individual item scores (7). Unfortunately, the total summed scores from rating scales simply offer rank-ordered values, as the component items are based on ordinal rating scales. Summing the scores from multiple items to create a total score is based on the assumption that all the items are measured on the same interval scale and each item contributes equally to the final score, irrespective of how well each item contributes to the underlying construct (8). Such summative scores often ignore the reality that some items may be more important in measuring a construct than others, especially when the difficulty levels of items are likely to be varied (9). Thus, the total summed scores obtained from rating scales violate the fundamental assumption of an equidistant interval (i.e. constant unit of measurement), which is required for the application of any parametric statistics (10).

Ordinal data generated from rating scales can be analysed using parametric statistics, which are more powerful than non-parametric statistics (11). However, when parametric statistics are applied to ordinal data the inferences about the underlying construct may not be logically valid and the resulting conclusions may therefore be misleading (12, 13). Previous research has demonstrated how the use of parametric statistics (e.g. analysis of variance (ANOVA)) with ordinal scores to compare groups can lead to incorrect inferences about the underlying construct level (14, 15) and spurious interaction effects between groups and conditions (16). Using a Monte Carlo simulation, another study also showed that untransformed summative ordinal scores can produce underestimated main effects and spurious interaction effects in the context of 2-way ANOVA, and may lead to misleading conclusions (17). A more recent study presented evidence that erroneous conclusions can occur when parametric statistics are applied inappropriately to analyse ordinal outcome measures from health-related quality of life measures (18).

In recent years Rasch models have been increasingly applied to operationalize rating scales due to their unique advantages over classical test theory (CTT) approaches (19). The Rasch model provides a means for transforming ordinal rating scale data into interval measures if and only if the data fit the model assumptions (20, 21). Under the Rasch algorithm, measurement errors can be estimated more accurately and the resulting scores hold the properties of sample independence, invariance and additivity (i.e. equality of the measurement at different points on the continuum). Previous research has suggested that scoring based on Rasch methods offers greater accuracy, precision and responsiveness than classical summative scoring when measuring patient outcomes based on ordinal rating scales (22–24). In addition, item characteristics from Rasch analyses are not necessarily sample dependant, as they are in classical test theory analyses, due to the separate estimation of item difficulty and person ability in Rasch analysis when using conditional estimation (22). Despite these advantages, little is known about the inferential benefits of applying Rasch modelling to analyse ordinal rating scale data in clinical practice and research.

In this paper, a Monte Carlo simulation study was designed to examine whether summative ordinal and Rasch-based interval approaches to scoring rating scales could lead to different statistical inferences when parametric statistics were employed to compare change scores between groups. More specifically, we sought to explore whether the inferential differences (if any) between the 2 scoring approaches were associated with the difficulty levels of test items, the ability of the respondents, or the size of the sample.

Methods

A Monte Carlo simulation study was designed to examine, when parametric statistics were operated, the impact of using the classical summative scores on inferences related to group comparisons of changes and whether such inference was comparable with that of using Rasch-based interval measures. The rationale for using a Monte Carlo simulation methodology was its flexible manipulation, whereby the rating scale responses could be generated under different simulation scenarios with distinct and known distributions of item difficulty and person ability with different sample sizes, which would otherwise be impossible to achieve in a clinical dataset (25). In this study, 3 populations with varying latent abilities (e.g. low, medium and high) were artificially generated, using the item response theory generation software WinGen (26). In particular, in each ability-level population, we generated one treatment group and one control group with a distinct mean difference, in order to present 3 different magnitudes of treatment effects. Polytomous ordinal responses with varying difficulty and ability parameters were generated using the Rasch partial credit model (PCM):

where θ is the ability for person on the construct and b is the item difficulty parameters for each score category with where is the difficulty of item i, and is the relative difficulty of score category x of item i.

For this simulation study, 3 tests with different item difficulty levels (e.g. easy, moderate and hard) were specified and each test included 10 items (as used elsewhere (27)). Response options for the items were fixed at 5 levels (0–1–2–3–4) to reflect scales commonly used in health and behavioural assessments (27). The items in the 3 tests were sampled from normal distributions (as used elsewhere (28–30)), with standard deviation of 1 and means of –1.0, 0.0, and 1.0, respectively, for easy, moderate and hard tests.

For each population, pseudo subjects were generated for 2 groups (i.e. treatment and control group) from normal populations with standard deviation (SD) of 1.0, but varying means. To ensure equal latent ability change (k) between the 2 groups (treatment and control) within each population, the treatment group mean was specified as the control group mean + k. A relatively small ability change (e.g. k = 0.3 for this analysis) was assumed to demonstrate how the 2 scoring approaches act in identifying small group differences under different simulation scenarios. Ability distributions of control groups in each population were generated from normal distributions with SD of 1 and means of –0.65, –0.15 and 0.35, respectively (Table I). Such distributions for treatment groups were generated from normal distributions with SD of 1 and means of –0.35, 0.15 and 0.65, respectively. Three sample conditions (n = 250, 500 and 1000), as used in other simulation studies (27, 31), were considered to generate subjects from normal distribution for the present study, with a set of 20 replications for each scenario.

Generated item responses for each test were summed in order to derive the raw total scores for each subject, referred to as classical summative scores (range 0–40). To derive the corresponding interval scale scores, Rasch PCM analysis was used. Specifically, we pooled the item responses from the control and treatment groups (at the same test difficulty level) together in each Rasch analysis (as described elsewhere (23, 32)). Thus the Rasch-produced ability estimates of each respondent across the control and treatment groups were anchored on the same measurement continuum of item difficulty parameters. These Rasch-based ability estimates were expressed in log-odd units or logits, which can be viewed as interval scores (4). As the data for this simulation study were generated using a unidimensional PCM model, no attempt was made to examine the Rasch model assumptions (e.g. unidimensionality, fit statistics). Details about the examination of Rasch model assumptions and derivation of logit scores (i.e. measures) from rating scales are given elsewhere (33, 34). Winsteps software V 3.68.2 (35) was used to perform the Rasch PCM analyses using joint maximum likelihood estimation.

Observed treatment effects were calculated by subtracting the mean score of the control group from that of the treatment group for each of the 3 populations (e.g. low, medium and high ability) under 3 different test conditions (e.g. easy, moderate and hard). A 1-way ANOVA was conducted to examine whether the treatment effects varied across the 3 populations under 3 different test conditions. Post-hoc pairwise comparisons with Bonferroni’s adjustment were further attempted in order to identify the pairs (if any) that were significantly different under the 2 scoring approaches. These analyses were independently implemented on the classical summation scores and the Rasch-based interval measures in order to examine whether the conclusions based on the 2 scoring approaches were different under the 3 samples with varying sizes: 250, 500 and 1,000.

Results

Figs 1a, b and c present the mean differences in change scores along with their error bars between the treatment and the control groups for each of the 3 populations (e.g. low, medium and high ability) under 3 different test conditions with sample sizes of 250, 500 and 1,000. While a constant change of 0.3 in ability between the treatment and control groups was set in the generation of their item responses, the observed changes in summative score were found to be different for various populations depending on the test difficulty levels. For summative scores (as shown in Fig. 1), easy tests with low ability consistently produced the highest differences in change scores compared with the easy tests applied to the groups with medium or high ability. By contrast, the highest mean difference in summative change scores for hard tests was found in the population with high ability level. This pattern was consistent across the 3 sample size scenarios. However, it is noted that the moderate tests applied to the population with medium ability had the highest mean difference only in the sample size of 250. It is thus implied that the magnitude of the mean differences in change scores of summative scores within each population might be dependent on the interactive relationship between test difficulty, respondent ability levels, or sample size.

For Rasch-based measures (as shown in Fig. 1), no consistent pattern regarding the difference in change scores was observed across the 3 difficulty tests applied to groups with 3 ability levels in 3 sample size conditions. However, it was found that the changes in Rasch-based measures marginally exceeded the simulated change value of 0.3 in most of the scenarios.

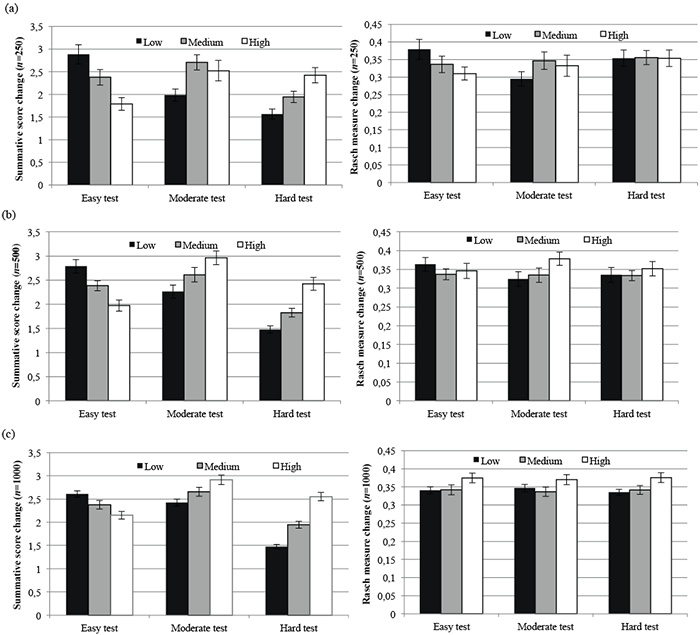
Fig. 1. Mean differences in change scores between treatment and control groups in classical summative scores and Rasch-based measures under different test conditions for a sample of (a) 250, (b) 500 and (c) 1,000.

One-way ANOVA revealed significant mean differences in change scores across the 3 population groups with low, medium and high ability when summative scores were considered for easy (p ≤ 0.001), moderate (p < 0.05) and hard (p < 0.001) tests for each sample size scenario. On the other hand, no statistical significance was identified when the same analyses were implemented on Rasch-based measures (p > 0.05) (Table II). Post-hoc pair-wise analyses on summative scores identified significant differences between population groups with low vs high ability (p < 0.01) in all sample size scenarios with the exception of the moderate test with a small sample size of 250.

Discussion

This study examined the extent to which the application of parametric statistics to classical summative scores generated from rating scales could produce conflicting inferences compared with Rasch-based measures. The results revealed that scaling artefacts could arise when using classical summative scores instead of Rasch-based interval measures. More specifically, the greatest difference in the summative scores was observed if the test with different difficulty levels was used in the participants with the corresponding ability levels (e.g. the easy test for the population with low ability or the hard test for the population with high ability). However, given that the data generated were pre-determined to have equal differences in latent abilities between the groups, it is evident that such observed differences could have resulted from the scaling artefacts; and a similar finding has been previously reported elsewhere (29). Earlier research also suggests that total summative scores are not linearly related with the underlying abilities, and that such non-linearity is influenced by the difficulty levels of test items (36). The author argued that non-linearity could be largest for abilities that are extreme with respect to the test items, presenting a plausible reason for differential changes in summative scores across various difficulty levels of test items.

The present study found that comparisons of different groups with different test difficulty levels produced conflicting inferences when using classical summative scores as opposed to Rasch-based measures. These findings are consistent with the findings of previous research, which has demonstrated that group comparisons using t-tests on an observed variable can be influenced by the difficulty of tests (14) and that inconsistent inferences about a latent variable can result from factorial ANOVA (15). The conflicting findings of the present study are therefore of interest, especially because the Rasch model, once fitted properly, can generate interval-level estimates that are suitable for parametric analysis and are more precise than summative scores (24).

In contrast to the findings of the present study, a recent study demonstrated that the use of summative scoring appeared robust to violations in the underlying assumptions of parametric analyses and is comparable to the item response theory-based scores when evaluating the relationships between test scores and outcome measures (27). In addition, there is evidence to suggest that although each item in a rating scale reflects an ordinal number, aggregation of such items into a single score to measure a construct may yield, or closely approximate, an interval scaled score (37), and thus facilitates the use of parametric statistics when analysing summative rating scale scores.

While Rasch-based measures have theoretical and potentially clinical advantages over summative scores, deriving Rasch measures requires choosing and applying the appropriate Rasch model with its underlying assumptions. This complicates the operationalization of Rasch modelling to transform summative scores into interval level measurements and may deter researchers and clinicians from using a Rasch-based scoring approach. More research is therefore warranted to either simplify the Rasch transformation process (e.g. by generating a transformation table) or delineate the conditions under which summative scores can be considered as interval measures and hence be appropriately subjected to parametric analyses.

In conclusion, the present study demonstrated that spurious statistical inferences are likely when analysing rating scale data with different item difficulty levels using classical summative scores, and that this has the potential to produce conflicting conclusions when comparing populations with respect to the underlying construct. Given that Rasch-based measures are generally considered an improvement over classical summative scores, this simulation study provides additional evidence for the use of Rasch-based scoring of rating scale data in order to make valid and accurate inferences through applying appropriate statistical analyses. These findings also support the argument of a recent editorial for not using raw scores from ordinal scales in rehabilitation sciences (38). Nevertheless, further real-world evidence is needed to support the findings of this simulation study and to motivate healthcare professionals and researchers to use a Rasch-based scoring approach when rating scales are used to assess patient-reported outcomes.

AcknowledgEments

This study was partly supported by a research grant from The University of Queensland, Australia. The authors would like to thank Dr Nicola W. Burton for her comments in an earlier version of this paper and Mr Onwell Maconi for helping with the simulation study.

References